Legendrian knot

In mathematics, a Legendrian knot often refers to a smooth embedding of the circle into 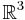\mathbb R^3, which is tangent to the standard contact structure on 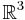\mathbb R^3. It is the lowest dimensional case of a Legendrian submanifold, which is an embedding of a k-dimensional manifold into a (2k+1)-dimensional that is always tangent to the contact hyperplane.

There can be inequivalent Legendrian knots that are isotopic as topological knots. These can be detected by considering their Thurston-Bennequin invariants and rotation number, which are together known as the "classical invariants" of Legendrian knots. There are also more sophisticated invariants of Legendrian knots constructed combinatorially by Chekanov and using holomorphic discs by Eliashberg. This Chekanov-Eliashberg invariant yields an invariant for loops of Legendrian knots by considering the monodromy of the loops. This has yielded noncontractible loops of Legendrian knots which are contractible in the space of all knots.

Any Legendrian knot may be C^0 perturbed to a transverse knot by pushing off in a direction transverse to the contact planes. The set of isomorphism classes of Legendrian knots modulo negative Legendrian stabilizations is in bijection with the set of transverse knots.

See also

References